この記事は Stan Advent Calendar 2020 の12月3日の記事です。
第1日目：Stanの導入
第2日目：Stanコードの構造と基本的な書き方

3日目は「平均値を推定してみよう」というテーマです。では、さっそく、平均値を推定しましょう。

※間違っている点がありましたら、ご指摘いただけますと幸いです。

例題（規定量でご飯をつげているのか）

学生時代に定食屋さんでアルバイトをしていたのですが、そのときご飯の量は並盛で200g (うろ覚え) でつぐように指導されました。そして、許容される誤差は10g (うろ覚え) でした。

店主の立場で「アルバイトの僕がきちんと規定量のご飯をつげているのか」ということをチェックするということを考えます。

とりあえず10食分ご飯をついでもらうことに

その結果、以下の値を得ました。

203 208 203 208 198 201 209 195 201 202

10食分のご飯の量を平均すると、202.8gでした。また、10回とも許容範囲内でした。このことから、「いいね。 こんな感じで明日もよろしくね 。」と伝えて解散するかもしれません。

明日も同じように？

ふと思います。「たしかに、テストした10回では許容範囲内だったけど、明日はどうだろうか。次は250gついでしまうかもしれない。明日も確認しないといけないな。」

こうして不安に駆られた店主は、 毎食毎食、きちんと定められた量がつげているかを確認することにしました。おしまい。

データ生成過程についての推測

店主が駆られた不安はよくわかります。たしかに、「これまでご飯を適切についできた」としても、そのことが「次のご飯を適切につぐ」ことを保証してくれるわけではありません。しかし、その不安に駆られてしまうと、すべてをチェックしなければなりません。

アルバイトさんがついだご飯をすべてチェックせずに、安心して任せるためには、アルバイトさんが「ご飯の規定に適切に従っているか」ということを確認する必要があります。

真のデータ生成過程

アルバイトさんが実際に従っている（と考えられる）ご飯つぎの規則を「真のデータ生成過程」と呼ぶことにします。実際には、アルバイトさんは何の規則にも従っていないかもしれませんが、「アルバイトさんに実際についでもらったご飯の量は、真のデータ生成過程から生成されている」と考えることで、まだついでいないご飯の量についても何らかの推測をすることができるようになります。真のデータ生成過程自体を考えない場合には、アルバイトさんがなんらかの規則に従っていると考えないことになるので、先の店主の様に、毎食毎食ご飯の量を確認することになるでしょう。

分析者が想定するデータ生成過程に関するモデル

得られたデータの背後にあると想定される「真のデータ生成過程」は直接観察することができません。そこで、分析者は真のデータ生成過程について、なんとか推測しようとします。そこで使用されるのが分析者が想定するデータ生成過程に関するモデルです。

今回の例では、確率モデルとして正規分布の確率密度関数を利用して、データ生成過程に関するモデルを構成することを考えます。正規分布を利用するのは、 分析者の想定にすぎません。ただし、モデルの構成の妥当性は、その問題についてのドメイン知識を利用して、共同体で判断されることになるので、何らかの制約はかかると思います。

ご飯データがアルバイトさんの(未知なる)真のデータ生成過程から生成されたとし、分析者が想定する確率モデルとして正規分布を利用します。正規分布は平均パラメータmuと標準偏差パラメータsigmaの2つをもちます。この2つのパラメータそれぞれが従う確率分布を設定します。これを事前分布と呼びます。事前分布も分析者の想定として設定されるものです。

データを観察して、モデルのパラメータの分布を更新する

データ観察前に分析者の想定として構成した、データ生成過程に関するモデルを観察したデータにあてはめて、「データが得られたときのパラメータが従う確率分布」を得ます。これを事後分布と呼びます。

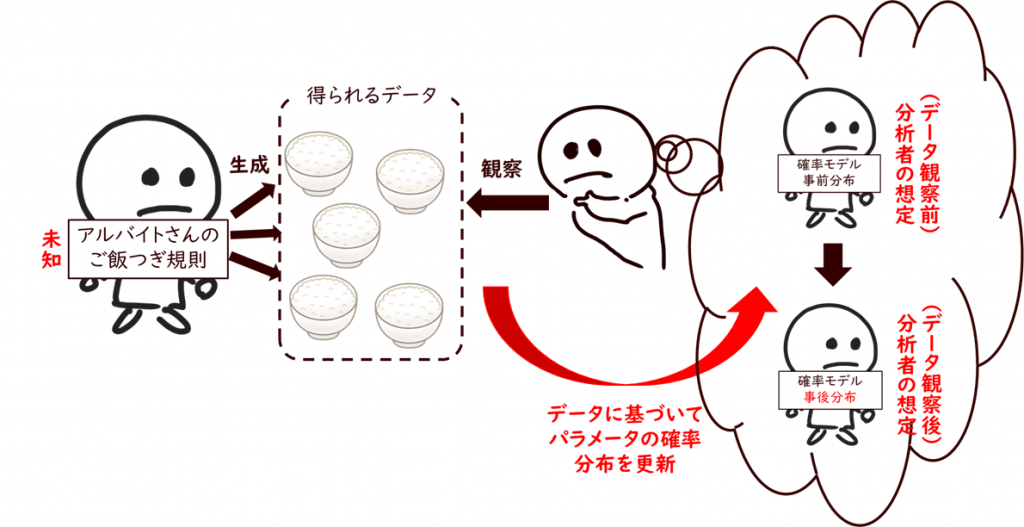
Stanをつかって、確率モデルと事前分布からなるデータ生成過程に関するモデルをでーたにあてはめて、事後分布を得ることができます。イメージとしては、下の図です。

本題：平均値について推測してみよう

ようやく本題です。今回は正規分布を利用してモデルを構成しました。モデルの平均パラメータをデータを使って更新して、アルバイトさんが平均して200gでご飯をついでいそうかということを推測します。また、今回の例では、たとえついだご飯の平均が200gであっても、茶碗にご飯がつがれていなかったり、ドラゴンボールなみにつがれているような場合には困るわけです。許容される誤差は10gでしたから、そのあたりのご飯をつぐ量のばらつきについても推測できると嬉しいです。正規分布の標準偏差パラメータも、データに基づいて更新するので、標準偏差パラメータも確認することにしましょう。

※実践部分について、結果の出力はrstanパッケージの関数を使っています。結果の可視化については、他にいろいろやり方があります。たとえば、bayesplot パッケージを用いたものについては、北條大樹さんの記事や
das_Kinoさんの記事があります。 翌日以降のアドカレも参照してください！

Stanコード

第2日目：Stanコードの構造と基本的な書き方を参照して、Stanコードを書いてみましょう。

できあがったStanコードがこちらです。名前を付けて、Stanファイルとして保存しましょう。例では、rice.stanとして保存しました。

data{
  int N;
  real Y[N];
}

parameters{
  real mu;
  real<lower = 0> sigma;
}

model{
  for(n in 1:N){
    Y[n] ~ normal(mu, sigma);
  }
  mu ~ normal(250, 200);
  sigma ~ student_t(4, 0, 5);
}

model部分では、①データYがパラメータmuとsigmaをもつ正規分布(normal)に従う、②パラメータmuは正規分布(mu=250, sigma=200)に従う、③パラメータsigmaは自由度4の半t分布(mu=0, sigma=5)に従う、という想定を反映させています。パラメータsigmaについては、parametersブロックで<lower=0>と記載することで、下限を0に指定しています。
パラメータの事前分布については、茶碗の大きさなどから、ご飯の量はほとんどの場合に50gから450gに収まるであろうという想定を反映させて、平均を250と設定しました。とはいえ、想定の範囲外にも対応できるように、標準偏差を200に設定して、想定の範囲に±1SDをあてて、想定の範囲外にも幅を持たせています。

実行してみる

data <- list(N = 10, 
             Y = c(203, 208, 203, 208, 198, 201, 209, 195, 201, 202))

model <- stan_model("rice.stan")

fit <- sampling(model, data,
                chains = 4, iter = 2000, warmup = 1000, thin = 1)

推定自体は一瞬で終わります。

ここで、sampling関数の引数について、説明をしておきます。

• chain: 発生させるMCMCの数（chain）を設定します。のちに、MCMCが収束しているかどうかを確認しますが、その際に、複数のMCMCを走らせておく必要があります。デフォルトは4です。
• iter: 1つのMCMCの中の乱数の個数を設定します。デフォルトでは2000が設定されていますが、収束状況が悪ければ、増やしたりします。
• warmup: MCMCの乱数の初めから何個を捨てるかを設定します。乱数生成は初期値に依存するので、最初の部分を切り捨て、収束してからの乱数を使って、事後分布を評価します。デフォルトではiterの半分です。
• thin: 間引きの数です。thinを2とした場合、乱数2個のうち1つを利用します。thinを5にした場合、乱数5個のうち1つを利用します。乱数の自己相関を抑える際に利用されたりします。僕はこれまで使っていないのでよくわかりません。

最終的に得られるMCMCサンプル数は、chain×(iter-warmup)/thinとなります。今回の設定だと、4×(2000-1000)/1＝4000のMCMCサンプルが得られます。

収束診断

トレースプロットの確認

まずやるべきことは、この推定が上手く行ったのかを確認する作業です。複数のMCMCチェインを走らせることで、それぞれが同じような範囲を動いているのかを確認します。 視覚的な確認として、トレースプロットをみてみます。traceplot関数を使用します。複数のチェインが事後分布からの乱数を得ているなら、サンプルは重なるはずです。

traceplot(fit)　#バーンイン期間含まない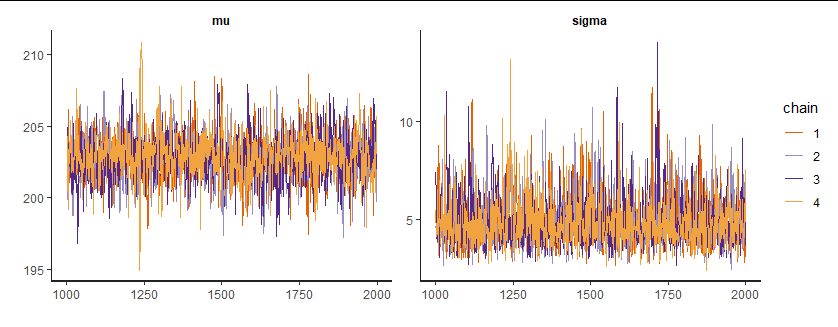

モデルのパラメータは2つですから、トレースプロットが2つ出ています。4本のチェインが重なっているので、収束していると判断できそうです。ついでに、バーンイン期間を含めたトレースプロットも確認してみましょう。

traceplot(fit, inc_warmup = T)　#バーンイン期間含める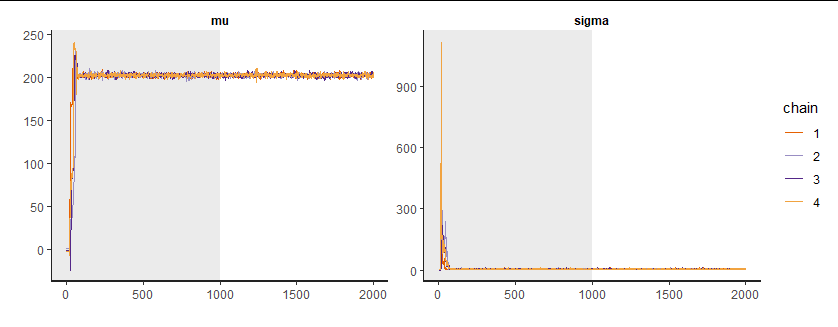

最初の100個くらいは初期値に依存していることが見て取れます。

確率密度プロットの確認

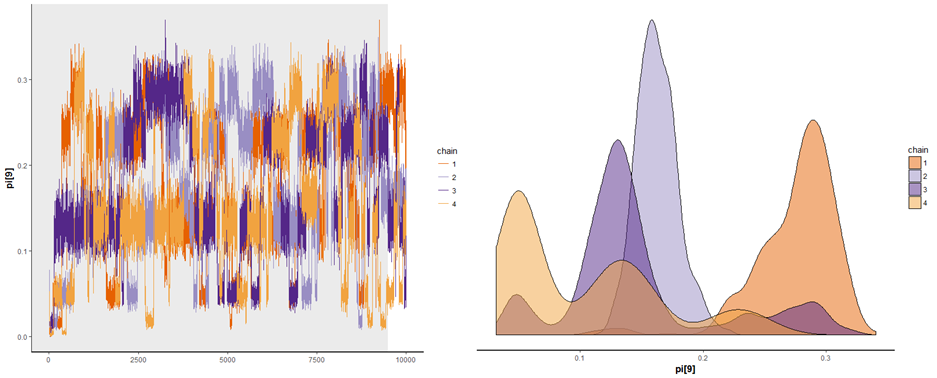
また、4つのチェインのそれぞれの事後分布を重ね合わせて、確認する方法もあります。stan_dens関数を使用します。これもトレースプロットと同様、収束しているなら、各チェインのサンプルは重なり合うはずです。

stan_dens(fit, separate_chains = T)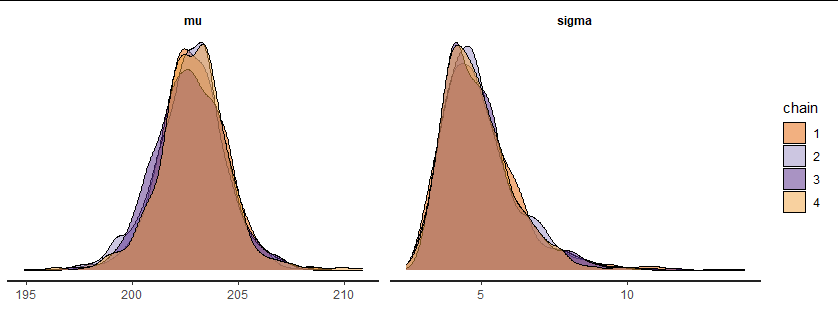

うまく収束しています。「ちょっとずれてる気がするけど、、」と思うかもしれません。全然ダメな例も見ておきましょう。

Gelman-Rubin統計量の確認

数値による収束判断の指標として、 R_hatがあります。「チェイン内の分散に対してチェイン間の分散がどれくらい大きいか」の指標で、完全に収束した場合に1.0となり、乖離したチェインがあれば1.0以上の値になります。1.1未満であることが必要です。

結果を格納したオブジェクトを見てみましょう。

fit

事後分布の確認

うまく収束していることがわかったので、事後分布をみてみましょう。先に述べたように、事後分布は 「データが得られたときの設定したモデルのパラメータが従う確率分布」です。 データを上の結果を格納したオブジェクトを開いた際に、事後分布について、平均やパーセンタイル点の情報が示されています。

今回は、アルバイトさんのご飯つぎ規則について、正規分布を利用して、その平均パラメータを推測することをしました。規定では、並盛は200gです。

事後分布の平均値(事後期待値; EAP)は、202.82でした。また、事後分布の中央値(事後中央値; MED)は、202.83でした。この他、事後分布において確率が最大となる点(事後確率最大値; MAP)を報告することもあります。

パラメータについて、幅のある推定（区間推定）をしましょう。事後分布の2.5％点から97.5%点に該当する範囲を調べることで、95％ベイズ信頼区間を得ることができます。 2.5％点が199.40、97.5%点が206.09でしたから、想定したモデルにおいて、アルバイトさんのご飯をつぐ量の平均パラメータの95％ベイズ信頼区間は、199.40－206.09となります。平均的には、200gに近い値をつぐような規則に従っているのではないかと推測できそうです。
せっかくなので事後分布の形状を確認しましょう。Stan_dens関数を使用し、すべてのチェインをあわせて表示します

stan_dens(fit, separate_chains = T)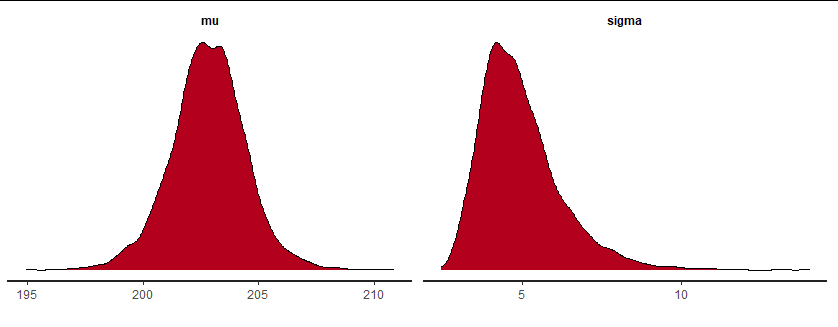

20201203追記：
以降の記述について、ご指摘をいただき、自分の理解が曖昧であったことがわかりました。確認して、適切な形に修正したいと思いますので、とりあえず取り消し線を引いていおります。申し訳ありません。ご指摘をありがとうございました。

事後予測分布でこれからのデータを予測

アルバイトさんの平均的なご飯をつぐ量は、200gになるような規則に従っていると考えてもよさそうだと判断しました。しかし、お店の規定では、平均的に200gであるだけでは十分ではなく、そのばらつきが小さくなければいけません。具体的には規定としては、±10gが求められます。

そもそも、店主が知りたいのは、平均的なご飯をつぐ量ではなく、そのアルバイトさんがつぐご飯の量がどのような分布になるのかということかもしれません。アルバイトさんのご飯をつぐ量が従っている真のデータ生成過程に関して、正規分布を利用してモデルを構成し、データに基づいて、モデルのパラメータの確率分布を更新しました。更新したモデルから、データを発生させ、その分布がどうなっているかを評価することができそうです。このような分布を事後予測分布といいます。データで更新したパラメータの分布ではなく、データで更新したパラメータを用いた、これから得られるであろうデータについての分布です。分析者が想定したモデルが真のデータ生成過程のよいモデルになっていれば、今後アルバイトさんのご飯の量を測定した際に、事後予測分布で予測したデータに近いものが得られると期待されます。

事後予測分布を作成するために、Stanコードに generated quantitiesブロックを 追加します。

data{ int N; real Y[N]; } parameters{ real mu; real sigma; } model{ for(n in 1:N){ Y[n] ~ normal(mu, sigma); } mu ~ normal(250, 200); sigma ~ student_t(4, 0, 5); } generated quantities{ real Y_pred; Y_pred = normal_rng(mu,sigma); }

事後予測分布を描いてみました。

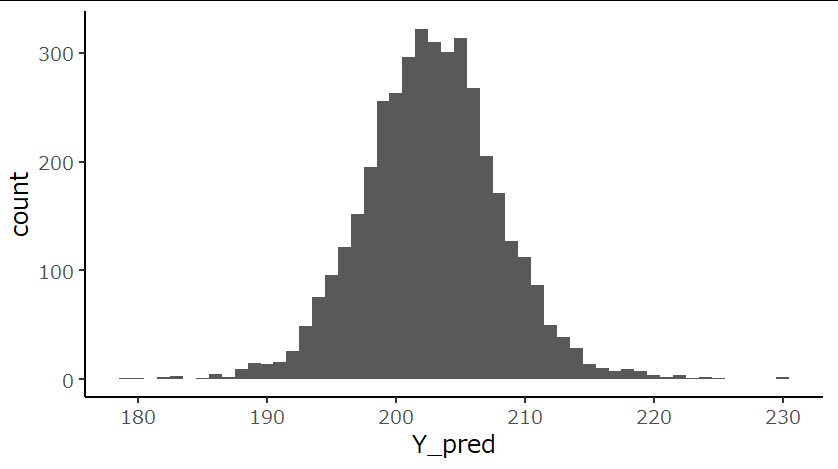
事後予測分布の平均値は202.8g、95％区間は192.6gから213.3gでした。また、許容範囲外の190g未満、210gを超える値の出現確率は、9％でした。

「だいたい良いんだけど、もうちょい気持ち少なめで、ブレが少なくなるようにね。」とアドバイスするかもしれませんね。

いかがでし(ry